题目链接
2019牛客多校第二场
background
出题人:sd0061
赵轩昂,北京航空航天大学,WorldFinal 2015/2016
Eddy
好像就是出题人的电脑用户名
出题评价
题目对我这个菜鸡来说较难,题意复杂
讲题评价
逻辑清晰,对每一题的讲解由浅入深,对时间复杂度不断优化精细讲解,层层入深,获得大家的一致好评(只是目前我这个菜鸡对于很多浅的地方还没学好甚至还没学过,所以补补补o(╥﹏╥)o)
A
题意
- Eddy大佬走路
先让0->N-1都有标记 -> 第i天走一圈需要Ni步(每天脚长不一样还行),可以前进和后退,然后收集完所有标记(每个地方都有标记,即0->N-1处都是标记)就立马感到无聊了就立马回去吃饭睡觉打豆豆(你的记录值中Eddy大佬走到Mi就算是收集完了所有的标记)
- 你每天观摩大佬走路(giao)
- 你复查数据的时候,你不确定到底数据是不是对的,然后你想知道这些天的数据正确的可能性(所以很自然的知道后面为什么要你输出前缀积,原来写笔记确实可以加深理解奥)
- T组测试(T天的观测)
- 然后每组测试都是给你Ni和Mi(每天Eddy的走路信息)
Output
- 输出前i天的数据都正确的可能性(也就是每天可能性之积)
思路
- Corner Case:
- 当N=1的时候,也就是1步就可以走完一圈,无论Eddy大佬前进还是后退,肯定是1步走完(这样肯定收集完了所有的标记),所以可能性为1
- 当M=0的时候,你记录的是Eddy大佬在0处就收集完了所有的标记,这是不可能,因为Eddy大佬一开始从0出发,所以一开始就已经拥有0号标记了,而一旦Eddy收集完所有的标记之后必定会立马回家,所以离开的地方的那个标记一定是最后收集到的,而且是第一次收集到的那个标记,所以你记录值为0显然是错的,所以可能性是0
- 一般情况(N非1,M非0)
- 有了上面M=0的理解,这里就好理解了,因为Eddy大佬一开始从0出发,然后Eddy大佬可以前进也可以后退,所以Eddy大佬最后一个到达的点可以是非0的其他任意一个点,所以最后到达每个点的可能性都是等概的,也就是
1/(N-1)
- 对了,输出的是前i的概率积
AC代码(自己再手写一遍收获更多)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod = 1e9+7;
int T,n,m;
ll ans;
ll mul(ll a,ll b){
a *= b;
return a>=mod?a%mod:a;
}
ll qpow(ll a,ll b){
ll ret = 1;
while(b){
if(b&1) ret = mul(a,ret);
/* b>>1,那么a就要变成a*a */
b>>=1;
a = mul(a,a);
}
return ret;
}
ll inv(ll a){ return qpow(a,mod-2); }
ll solve(ll n,ll m){
if(n==1) return 1;
if(m==0) return 0;
return inv(n-1);
}
int main(){
ios::sync_with_stdio(false);
/*init*/
ans = 1;
cin>>T;
while(T--){
cin>>n>>m;
/*solve*/
ans = mul(ans,solve(n,m));
cout<<ans<<endl;
}
return 0;
}
|
B
emmmm,看懂了一点点题解,但是对于题解中的BM完全不熟悉,所以先留坑
C,D自己太菜了,留坑
E
emmmm,看懂了一点点题解,但是还是不太熟悉基础的算法,我先去补基础的算法,留坑
F
题意
给定2N个人,(N <= 14),两两间有边权,把这2N个人分为2组,每组N个,求两组间的边权和最大
题解
朴素法(也称暴力法),在新加入一个人的时候,比如说加入了A组,那么直接将它与B组间已经有的所有人的边权加一遍
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 50;
int d[M][M];
int a[M],b[M];
int cnt1,cnt2;
ll ans;int N;
void dfs(int cur,ll val){
/*当达到2*N+1的时候,正好已经插入了2*N个人了,所以开始比较*/
if(cur>2*N){ ans = max(ans,val);return ;}
if(cnt1<N){
a[cnt1++]=cur;
ll tmp = 0;
/*每次加入了cnt1之后,就要把左边队伍新加人与对面队伍当下所有人产生的竞争值加入左边队伍*/
for(int i=0;i<cnt2;i++) tmp+=d[cur][b[i]];
dfs(cur+1,val+tmp);
/*上面的遍历return之后要恢复现场,即之前产生的影响要消除掉,避免对后面的操作有影响*/
cnt1--;
}
if(cnt2<N){
b[cnt2++]=cur;
ll tmp = 0;
/*每次加入了cnt2之后,就要把右边队伍新加人与对面队伍当下所有人产生的竞争值加入右边队伍*/
for(int i=0;i<cnt1;i++) tmp+=d[a[i]][cur];
dfs(cur+1,val+tmp);
cnt2--;
}
}
int main(){
ios::sync_with_stdio(false);
cin>>N;
for(int i=1;i<=2*N;i++)
for(int j=1;j<=2*N;j++)
cin>>d[i][j];
ans = 0;
/*像一颗树一样遍历下去,然后到达叶子的时候进行比较出最大值再返回*/
dfs(1,0);
cout<<ans<<endl;
return 0;
}
|
G计算几何,留坑
H
题意
给定一个N*M的01矩阵(1<=N,M<=1000),求第二大全是1的矩阵面积
题解
- 枚举每一行,以当前行为底,记录每一列往上不间断最多延长多远,那么这样之后就变成了一维的柱状图求最大/次大/k大矩形面积,可用单调栈求解
- 由于要记录第二大,之前求最大的做法(poj2559)是直接用max维护ans,width合并的做法在这里就要改成把所有解先丢进一个vector(之后排序复杂度
ans个数 * log(ans个数))(或者维护一个k大的小值优先的priority_queue,复杂度算上维护也是ans个数 * log(ans个数))
- 但是这里必须把
(width-1)*ddz[top]也放入状态级,因为求第二大,所以只要把次大状态加入(详细原因看下面说的坑点)
- 所以推荐使用把全状态扔进vector,这样还可以求第k大,虽然慢点
坑点
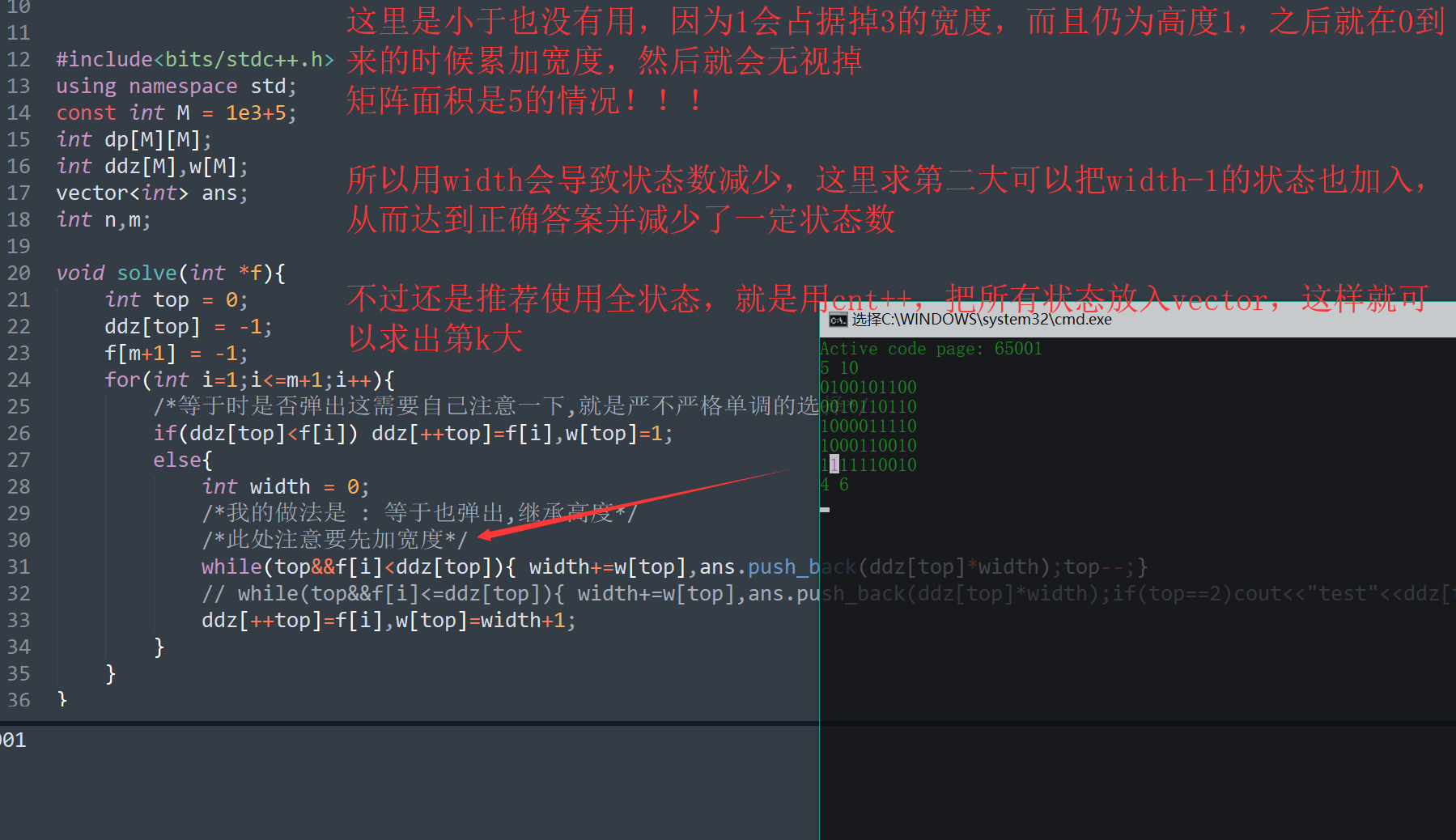
图中最后一行样例的dp的单调栈
这里是小于也没有用,因为1会占据掉3的宽度,而且仍为高度1,之后就在0到来的时候累加宽度 (宽度直接从4加到了6,跳过了5,因为1之前会占据掉3的宽度),然后就会无视掉
矩阵面积是5的情况!!!
所以用width会导致状态数减少,这里求第二大可以把width-1的状态也加入,从而达到正确答案并减少了一定状态数
不过还是推荐使用全状态,就是用cnt++,把所有状态放入vector,这样就可以求出第k大

AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
/*
5 10
0100101100
0010110110
1000011110
1000110010
1111110010
*/
#include<bits/stdc++.h>
using namespace std;
const int M = 1e3+5;
int dp[M][M];
int ddz[M],w[M];
vector<int> ans;
int n,m;
void solve(int *f){
int top = 0;
ddz[top] = -1;
f[m+1] = -1;
for(int i=1;i<=m+1;i++){
/*等于时是否弹出这需要自己注意一下,就是严不严格单调的选择*/
if(ddz[top]<f[i]) ddz[++top]=f[i],w[top]=1;
else{
int width = 0;
/*此处注意要先加宽度*/
while(top&&f[i]<ddz[top]){ width+=w[top],ans.push_back(ddz[top]*width),ans.push_back(ddz[top]*(width-1));top--;}
/*我的做法是 : 等于是加入,不严格单调*/
ddz[++top]=f[i],w[top]=width+1;
}
/*推荐下面的方法*/
// if(ddz[top] <= f[i]) ddz[++top] = f[i];
// else {
// int cnt = 0;
// /*然后这里可以写宽度进行优化*/
// while(top && ddz[top] > f[i]) {
// cnt++;
// ans.push_back(ddz[top] * cnt);
// top--;
// }
// while(cnt--) ddz[++top] = f[i];
// ddz[++top] = f[i];
// }
}
}
int main(){
char c[M];
while(~scanf("%d%d",&n,&m)) {
/*init*/
ans.clear();
for(int i=1;i<=n;i++){
/*对于每一列的每一行进行连续高度扫描*/
scanf("%s",c);
/*此行非0,则可以接上上面连续来的高度(可能为0)*/
for(int j=1;j<=m;j++) dp[i][j] = c[j-1] == '0'? 0 : dp[i-1][j]+1;
}
// for(int i = 1;i<=n;i++) {for(int j=1;j<=m;j++) cout<<dp[i][j]; cout<<endl;} cout<<endl;
/*solve*/
/*对每一行进行直方图扫描求解*/
for(int i=1;i<=n;i++) solve(dp[i]);
sort(ans.begin(),ans.end());
/*考虑特例*/
int sz = ans.size();
if(sz<=1) printf("0\n");
printf("%d\n", ans[sz-2]);
}
return 0;
}
|
I听Eddy大佬说有7种dp,太难留坑
J也太难留坑