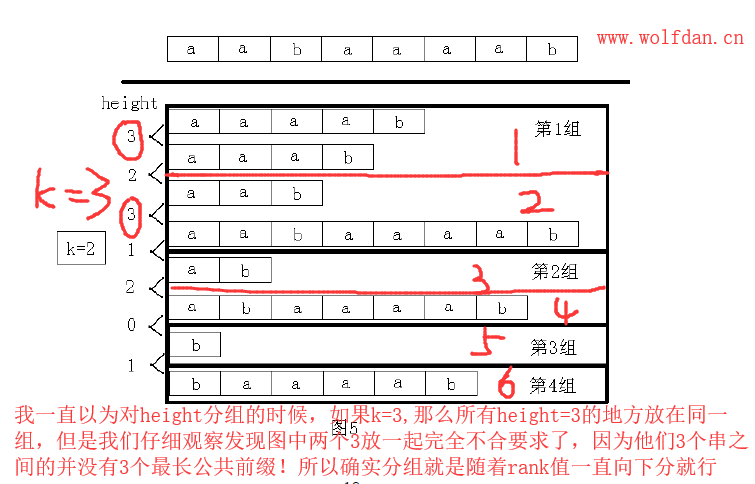
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
|
/*
今天在第二次研究hdu5008的时候,发现好多题目都是没有用rmq的
但是总有大佬不满足于暴力裸sa就完事,于是都加了rmq,
然后我有点看不懂,就去逛oi-wiki,发现居然有不重叠重复两次
的串也可以用rmq,那不就是我昨天做的poj1743的更优做法吗?
是的,然后就在网上搜到了O(test*(nlogn+logn))的做法!
之前的写法是O(test*nlogn)的
但是实测发现RMQ版的反而还慢了100多ms!好像是因为他的check还是O(n)而非O(1)的
因为这里的check是我们自己去寻找一个左右区间,而非输入直接给我们左右区间,
所以这里的寻找的复杂度是O(n),所以RMQ无济于补
而且RMQ是nlog(n)的预处理... 所以当然会慢啊 ---> 所以在更大一个量级的询问的时候再用比较好
----------------上面为简单分析-----下面为用途---------------
这里有rmq求排名区间内最远的sa位置差值
*/
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=21000;
int dp1[maxn][20],dp2[maxn][20];
int mm[maxn];
int str[maxn],tmp[maxn];
int wa[maxn],wb[maxn],wv[maxn],ws[maxn];
int sa[maxn],ranks[maxn],height[maxn];
inline bool cmp(int *r,int a,int b,int l){
return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int *r,int n,int m){
int i,j,p,*x=wa,*y=wb,*t;
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[x[i]=r[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;
for(j=1,p=1;p<n;j*=2,m=p){
for(p=0,i=n-j;i<n;i++) y[p++]=i;
for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0;i<n;i++) wv[i]=x[y[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];
for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
}
for(i=0;i<n;i++) ranks[sa[i]]=i;
int k=0;
for(i=0;i<n-1;i++){
if(k) k--;
j=sa[ranks[i]-1];
while(r[i+k]==r[j+k]) k++;
height[ranks[i]]=k;
}
return;
}
void initRMQ(int n){
/*mm其实是log,这里赋值为-1是为了后面mm[1]=0,也就是2^0=1*/
mm[0]=-1;
for(int i=1;i<=n;i++){
/*(i&(i-1))==0表示n==0或者是2的倍数*/
mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
/*这里是预处理sa的rmq*/
dp1[i][0]=dp2[i][0]=sa[i];
}
for(int j=1;j<=mm[n];j++)
for(int i=1;i+(1<<j)-1<=n;i++){
dp1[i][j]=max(dp1[i][j-1],dp1[i+(1<<(j-1))][j-1]);
dp2[i][j]=min(dp2[i][j-1],dp2[i+(1<<(j-1))][j-1]);
}
}
int rmq(int x,int y){
int k=mm[y-x+1];
return max(dp1[x][k],dp1[y-(1<<k)+1][k])-min(dp2[x][k],dp2[y-(1<<k)+1][k]);
}
bool check(int len,int N){
int s=1,e=1;
while(e<N){
if(height[e+1]>=len-1) e++;
else{
if(rmq(s,e)>=len) return true;
s=++e;
}
}
return false;
}
int main(){
int N;
while(scanf("%d",&N)&&N){
for(int i=0;i<N;i++)
scanf("%d",&str[i]);
for(int i=0;i<N-1;i++)
tmp[i]=str[i+1]-str[i]+90;
tmp[N-1]=0;
/*这里没有N--,所以直接使用的N,而RMQ使用的N-1,height封锁掉N号位置*/
da(tmp,N,200);
initRMQ(N-1);
height[N]=-1;
int left=1,right=N/2;
while(left<=right){
int mid=(left+right)/2;
if(check(mid,N)) left=mid+1;
else right=mid-1;
}
if(right<5) printf("0\n");
else printf("%d\n",right);
}
return 0;
}
|