Algorithm
lc553_最优除法
除的结果最大化 = 被除数最大化 + 除数最小化
作为被除数,就前一个大于后一个数,就不要想除
作为除数,就前一个小于后一个数,就多相除
动规吧, 看下答案
发现还有我观察到的规律的直接总结,哭了—动规生疏了,脑子也不灵活了,多训练吧,加油
链接:https://leetcode-cn.com/problems/optimal-division/solution/zui-you-chu-fa-by-leetcode-solution-lf4c/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
struct Node {
double maxVal, minVal;
string minStr, maxStr;
Node() {
this->minVal = 10000.0;
this->maxVal = 0.0;
}
};
class Solution {
public:
string optimalDivision(vector<int>& nums) {
int n = nums.size();
vector<vector<Node>> dp(n, vector<Node>(n));
for (int i = 0; i < n; i++) {
dp[i][i].minVal = nums[i];
dp[i][i].maxVal = nums[i];
dp[i][i].minStr = to_string(nums[i]);
dp[i][i].maxStr = to_string(nums[i]);
}
for (int i = 1; i < n; i++) {
for (int j = 0; j + i < n; j++) {
for (int k = j; k < j + i; k++) {
if (dp[j][j + i].maxVal < dp[j][k].maxVal / dp[k + 1][j + i].minVal) {
dp[j][j + i].maxVal = dp[j][k].maxVal / dp[k + 1][j + i].minVal;
if (k + 1 == j + i) {
dp[j][j + i].maxStr = dp[j][k].maxStr + "/" + dp[k + 1][j + i].minStr;
} else {
dp[j][j + i].maxStr = dp[j][k].maxStr + "/(" + dp[k + 1][j + i].minStr + ")";
}
}
if (dp[j][j + i].minVal > dp[j][k].minVal / dp[k + 1][j + i].maxVal) {
dp[j][j + i].minVal = dp[j][k].minVal / dp[k + 1][j + i].maxVal;
if (k + 1 == j + i) {
dp[j][j + i].minStr = dp[j][k].minStr + "/" + dp[k + 1][j + i].maxStr;
} else {
dp[j][j + i].minStr = dp[j][k].minStr + "/(" + dp[k + 1][j + i].maxStr + ")";
}
}
}
}
}
return dp[0][n - 1].maxStr;
}
};
|
推理总结
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
string optimalDivision(vector<int>& nums) {
int n = nums.size();
if (n == 1) {
return to_string(nums[0]);
}
if (n == 2) {
return to_string(nums[0]) + "/" + to_string(nums[1]);
}
string res = to_string(nums[0]) + "/(" + to_string(nums[1]);
for (int i = 2; i < n; i++) {
res.append("/" + to_string(nums[i]));
}
res.append(")");
return res;
}
};
|
Review
【TED演讲】如何为自己说话
不断学习,扩展自己的实力最重要
我们每个人都是有一个接受范围的,我们时而强势自我,时而懦弱不争。我们的这个域到底是如何界定的?事实上,这个范围并非固定不变,而是会随着语境变化而变化。那时那刻,你的实力在决定着你可接受范围的边界。
重点是,我们的实力小时,我们的行动就变得局限,比如畏手畏脚地做事、需要解决眼前问题但无能为力……这时处于“弱势两难”的境地,如果我们沉默不敢站出来为自己说话则会被忽视、问题得不到解决,如果我们说出来又会受到相应的惩罚(自不量力而失去机会等)。
如何扩大我们的可接受范围,增加我们的实力?两个重要的影响因素。一是你在自己眼中是实力者,这时你会感到更加自信、不会害怕,就会扩大自己的域;二是你在他人眼中是实力者,他们给予了你更大的可接受范围。
具体做法:①为他人声张时,我们就能发掘自己的声音,就像“熊妈妈效应”;②为自己讲话时换位思考,站在对方角度去想对方的需求,更容易产生自己真正想要的结果;③展现自己的灵活力,沟通时抛出选择题更能得到对方的yes;④向他人寻求建议获得盟友,当一个谦恭的咨询者,可以解决“自我推销两难”困境(不推荐则没影响力,推荐则不讨喜),因为就自己的成就征求意见在他人眼中会变得能干且讨喜;⑤掌握专业知识,提高可信度,发掘自身的热情。
Tips
TAILQ 队列之一二事
Share-TAILQ中一两个函数理解
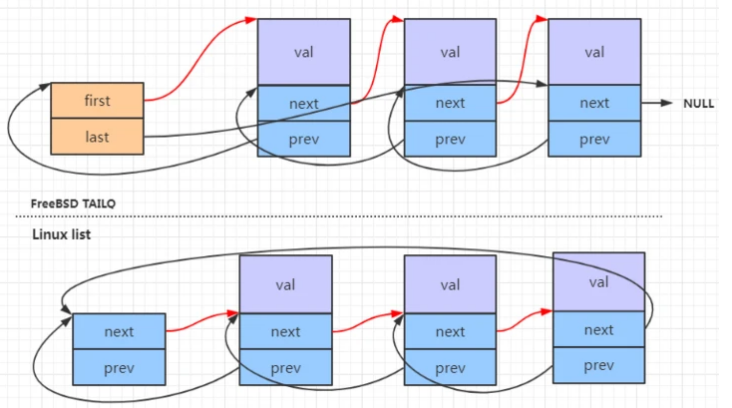
总体结构

必须熟悉这个结构,才好理解下面的队列操作,否则会完全不理解
删除一个元素
这个函数挺有趣的,就是*(elm)->field.tqe_prev = TAILQ_NEXT((elm), field); 比较难理解
这里其实就是因为*(elm)->field.tqe_prev 就是 ``*(elm)->field.tqe_prev`的next
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#define TAILQ_REMOVE(head, elm, field) do { \
QMD_SAVELINK(oldnext, (elm)->field.tqe_next); \
QMD_SAVELINK(oldprev, (elm)->field.tqe_prev); \
QMD_TAILQ_CHECK_NEXT(elm, field); \
QMD_TAILQ_CHECK_PREV(elm, field); \
if ((TAILQ_NEXT((elm), field)) != NULL) \
TAILQ_NEXT((elm), field)->field.tqe_prev = \
(elm)->field.tqe_prev; \
else { \
(head)->tqh_last = (elm)->field.tqe_prev; \
QMD_TRACE_HEAD(head); \
} \
*(elm)->field.tqe_prev = TAILQ_NEXT((elm), field); \
TRASHIT(*oldnext); \
TRASHIT(*oldprev); \
QMD_TRACE_ELEM(&(elm)->field); \
} while (0)
|
插入队尾
*(head)->tqh_last = (elm); 这里是把原来的队尾的next指针赋值为 新队尾
(head)->tqh_last = &TAILQ_NEXT((elm), field); 这里是把last 指针赋值为 新队尾的next的起始地址
1
2
3
4
5
6
7
8
9
|
#define TAILQ_INSERT_TAIL(head, elm, field) do { \
QMD_TAILQ_CHECK_TAIL(head, field); \
TAILQ_NEXT((elm), field) = NULL; \
(elm)->field.tqe_prev = (head)->tqh_last; \
*(head)->tqh_last = (elm); \
(head)->tqh_last = &TAILQ_NEXT((elm), field); \
QMD_TRACE_HEAD(head); \
QMD_TRACE_ELEM(&(elm)->field); \
} while (0)
|